【公開授業】中学1年生数学 ~比例の利用~

比例のグラフ「y=ax」の難問を徹底解説! 伝統的な虎谷の授業で「キライ」を「わかる」にしたいのだ!
< 学習のポイント >
① 問題文の意味を理解しよう。(点Pの移動を考える)
②「y=ax」の式を作ろう。(三角形の面積を求める)
③ 文章アレルギーを克服しよう。(読むのを諦めない)

早速ですが、このような難問は好きですか?よく出ますよね(笑)
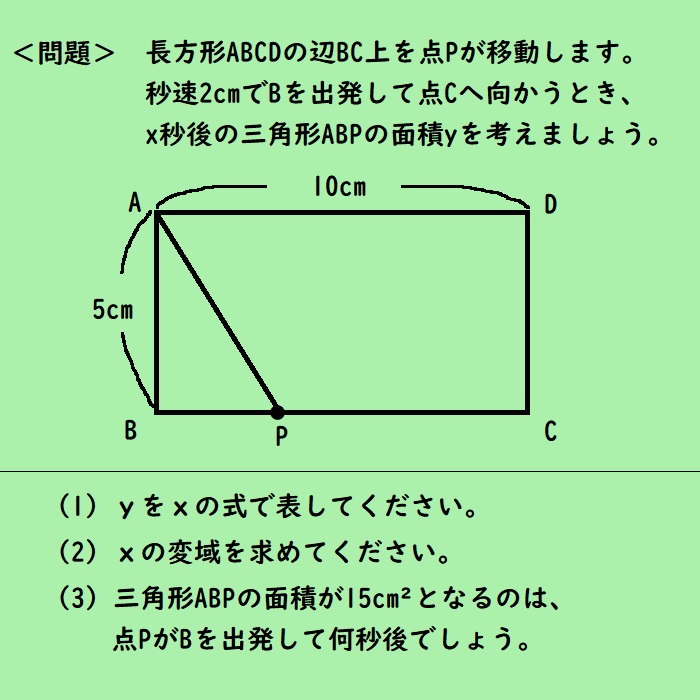

「ムリゲー!考えたくない」と思う人もいるでしょう?
今回はこの問題をじっくり解説したいと思います^^
まずは、このイラストを確認してください。
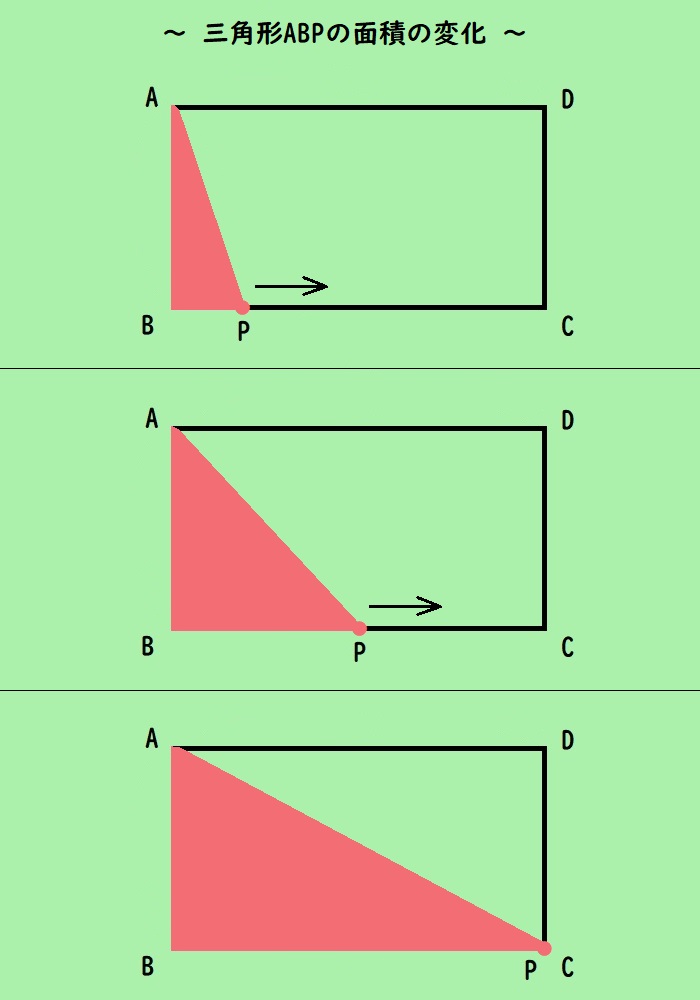

点Pが動くため、三角形ABPは大きくなっていきます。
このように、問題文を読んだらそのイメージをつかむのです。
(1)の解説 (yをxの式で表す)
① yは「三角形ABPの面積」
② xは「点Pが出発してからの秒数」
まず、この2点を問題文から読み取れますか?
①から、yは面積のことなので「y=なになに」の式を作ればよいのですね。
それと、図から「高さ5cm」がわかります。
三角形の面積の公式に高さ5cmも代入できるみたい。
「 面積 = 底辺 × 高さ ÷ 2 」は
「 y = 底辺 × 5cm ÷ 2 」となります。
下のイラストでここまでを整理しておきましょう!
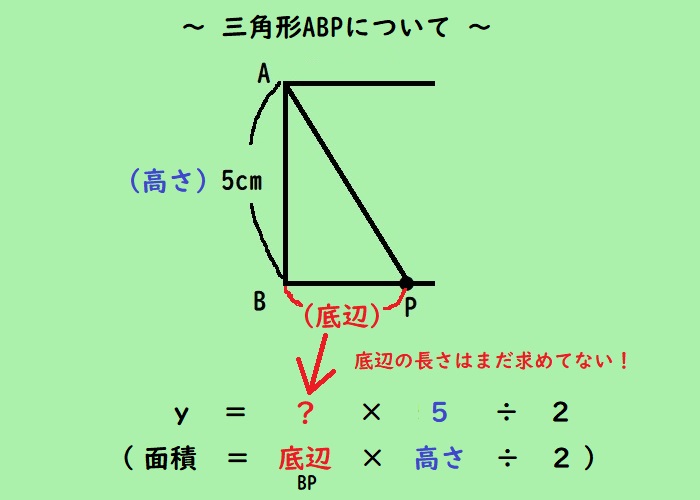
今度は、底辺の長さを考えてみましょう。(一番生徒を悩ませる部分)
とりあえずBPが底辺だとわかるはずです。でも長さは?
なんと点Pが動いているのですよ!「許せないッ!」
でも簡単。「底辺」=「秒速2cm」×「x秒」だと思いませんか?
1秒経つと底辺は2cm、2秒経つと底辺は4cmになることから考えればよいのです。
よって、底辺は「2x」とわかりました。
この底辺2xをさっきの式に代入すると、
y=底辺×5cm÷2
y=2x×5cm÷2
y=10x÷2
y=5x
(1)の解答は、y=5xでした!
(2)の解説 (xの変域を求める)

xの変域、なんそれ!?
変域とは「とりうる範囲」のこと。
ここでは「xがいくつからいくつまで変化するのか」を指します。
xと底辺の関係性を表にしてみましょう!
| x(秒) | 0 | 1 | 2 | 3 | 4 | 5 |
| 底辺BP(cm) | 0 | 2 | 4 | 6 | 8 | 10 |
x(秒)は0~5の範囲だとわかりますね。
・長方形の辺BC=10cm
・点Pの移動距離=秒速2cm×5秒で10cm
だからxが5(秒)を超えたら、点Pが長方形からポーンと飛び出します(笑)
つまり、xの変域が0~5なので「xは0以上で5以下」です。
これを不等式にすると「0≦x≦5」となります。
(2)の解答は、0≦x≦5でした!
(3)の解説 (三角形ABPの面積が15cm²の時、xを求める)
面積が15cm²になるということはy=15なのです。
だから、(1)で求めたy=5xにそのまま代入しましょう!
y=5x
15=5x ※yに15を代入。
x=3
(3)の解答は、3秒後でした!
< 最後に >
今回のよく出る難問、いかがでしたか?
【文章問題の解法】
「読解」→「作図・作表」→「立式」→「計算」→「解答」
この手順をふめば、どんな問題も必ず解けるようになりますよ。
まず、文章問題では読解から始めます。その内容から「イメージ」をつかむのです。
その後、何を求めるべきかがわかるので答えも出せるはず。

ではまた!
勉強、頑張っていきましょう!


